APLICACIONES DE LA INTEGRAL
ÁREA ENTRE DOS CURVAS
El área entre dos curvas f(x) y g(x) acotadas en x=a , y=b, está dada por:
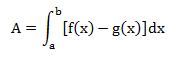

//valores de x
x=[0:0.01:1.2];
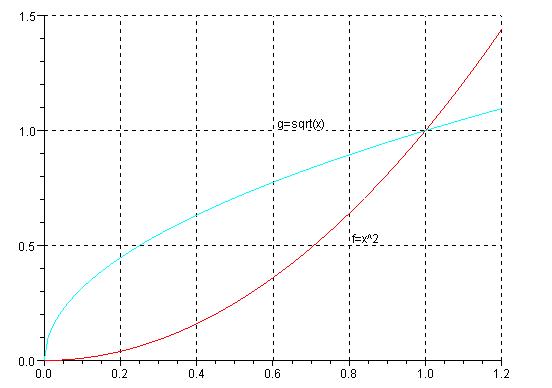
f=x^2;
g=sqrt(x);
plot2d(x,[f'g'],[5 4])
xset("font size",2)
xstring(0.8,0.5,["f=x^2"])
xstring(0.6,1.0,["g=sqrt(x)"])
xgrid

//cálculo del área entre las curvas
function y=f(x)
y=sqrt(x)-x^2;
endfunction
intg(0,1,f)
//ans=0.33
SÓLIDOS DE REVOLUCIÓN
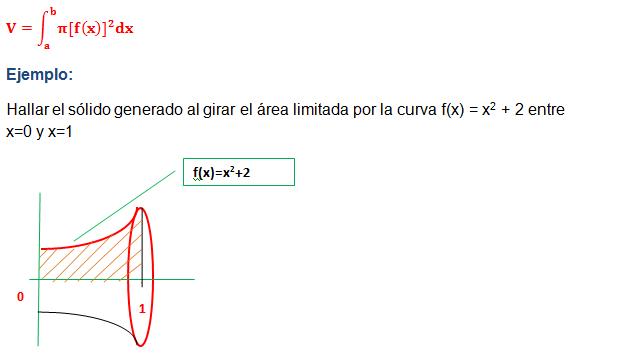
Un sólido de revolución se genera al girar un área alrededor de uno de los ejex cartesianos. Para un área limitada por f(x) y el eje x entre valores de a y b, el volumen es igual a:
 Por Scilab:
Por Scilab:
//la función es
function y=f(x)
y=%pi*(x^2+2)^2
endfunction
//cálculo del área
intg(0,1,f)
//ans = 17.38
LONGITUD DE ARCO
La longitud de arco de una curva dada por f(x) entre límites a y b, está dada por:

Gráfica con Scilab
//valores de x
x=[0:0.01:20];
y=2*sqrt(x)-2;
plot(x,y)
xgrid

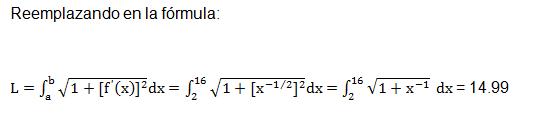
Usando Scilab:
//la función derivada es
function y=f(x)
df=x^(-1/2);
y=sqrt(1+df^2)
endfunction
//cálculo de la longitud
intg(2,16,f)
//ans=14.99
SUPERFICIE DE REVOLUCIÓN
La superficie de revolución generada al girar una curva f(x) alrededor del eje x entre los valores x=a y x=b, es igual a:
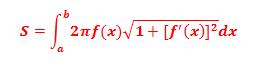
Ejemplo:
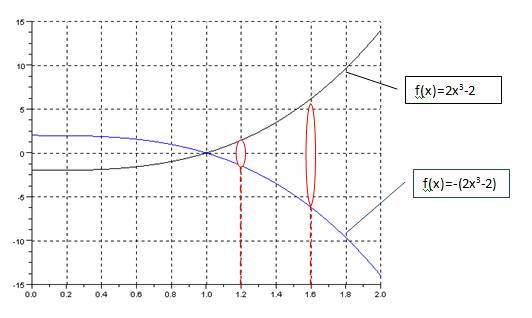
Hallar el área de la superficie generada al girar f(x)=2x3-2 alrededor del eje x entre x=1.2 y x=1.5
Gráfica con Scilab,
//valores de x
x=[0:0.01:2];
y=2*x^3-2;
y1=-(2*x^3-2);
plot2d(x,[y' y1'])
xgrid
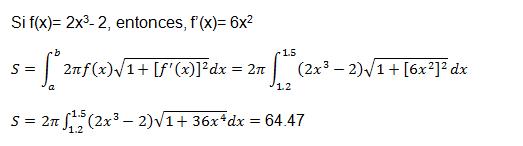
Calculando por Scilab:
//la función es
function y=f(x)
df=6*x^2;
y=2*%pi*(2*x^3-2)*sqrt(1+df^2)
endfunction
//cálculo del área de revolución
intg(1.2,1.5,f)
//ans=64.47