PARTE II. CORRIENTE ALTERNA
PRESENTACIÓN
En esta unidad, se estudiará la señal de corriente alterna, su frecuencia, amplitud, fase, capacitores o condensadores y el circuito capacitivo serie con ejemplos ilustrativos. Para el aprendizaje se tendrá la información teórica con algunos videos de soporte de Youtube, la simulación de circuitos usando el software Solve Elec que es muy sencillo libre y gratuito (open course) como laboratorio virtual y el laboratorio práctico para el desarrollo de los circuitos en protoboard. Terminada la unidad, el estudiante debe realizar la evaluación correspondiente.
UNIDAD 4: CIRCUITO CAPACITIVO
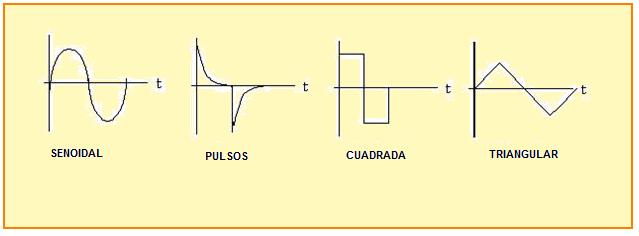
Entre las señales cuya amplitud varía regularmente al transcurrir el tiempo tenemos las señales senoidales, señales cuadradas, señales triangulares y señales en forma de pulsos.
FRECUENCIA
Un ciclo está formado por dos alternancias una positiva y una negativa.
Frecuencia (f) es el número de ciclos que ocurren en la unidad de tiempo. Se mide en Hertz (Hz). Periodo (T) es el tiempo de duración de un ciclo y se mide en segundos (sg). El periodo es el inverso de la frecuencia y viceversa.
T = 1 / f o f = 1 / T
Unidades del periodo:
1 milisegundo = 1 msg = 1sg / 10^3 = (10^- 3) sg
1 microsegundo = 1 usg = 1 sg / 10^6 = (10^- 6) sg
Unidades de la frecuencia:
1 kilohertz = 1 Khz = 10^3 Hz , corresponde a un periodo de 1 msg
1 megahertz = 1 Mhz = 10^6 Hz, corresponde a un periodo de 1 usg
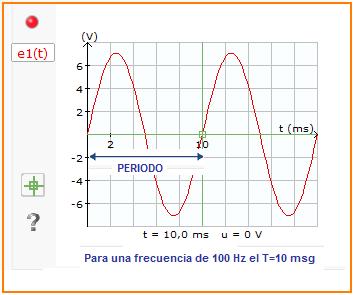
EJEMPLO
AMPLITUD
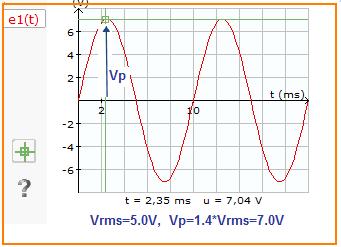
Es la magnitud de la señal y se mide en el eje vertical. Al valor máximo de una señal se le llama valor pico y al valor cresta a cresta se le llama calor pico a pico. Si la señal es de voltaje entonces sería : Valor pico = Vp, y el valor pico a pico = Vpp.
Un valor generalmente utilizado para medir una señal alterna es el valor rms o valor efectivo. En el caso de un multímetro es la medición que se hace al colocarlo en corriente alterna CA. El valor rms y el valor pico se relaciona mediante la ecuación:
Vp = 1.4 Vrms, Vrms = Vp / 1.4
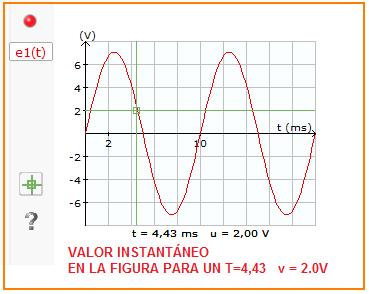
En forma general una señal alterna es descrita por una ecuación donde se refleje su magnitud, frecuencia y fase. La fase es el grado de corrimiento en grados que tiene una señal con respecto al eje vertical o a otra señal. En la figura de abajo, la señal roja e1(t) es una señal senoidal, en un tiempo t=0 su valor es cero por lo tanto se dice que su fase es de 0 grados. La señal azul u1(t) tiene un desfase con relación a e1(t). Para conocer su valor en grados se hace una relación teniendo en cuenta su desfase en tiempo. En la figura el desfase es de 1.39 sg. Como el periodo (tiempo en un ciclo) es de 10 msg que corresponde a un ángulo de 360 grados, su fase en grados es:
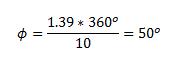
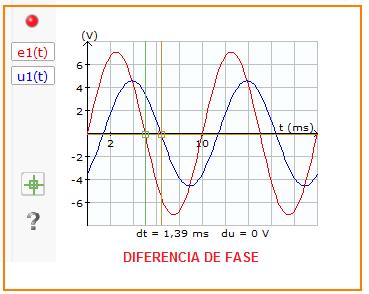
La ecuación general de representación de una señal alterna es de la forma:
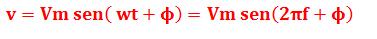
EL CAPACITOR
El condensador es un elemento utilizado en la electrónica encargado de almacenar voltaje a través de su campo eléctrico. Al aplicar una fuente de corriente continua E al condensador este se carga en forma exponencial partiendo de un valor cero hasta su valor máximo E y al desconectarse de esta fuente se descarga también en forma exponencial de este valor E hasta cero.
Los condensadores o capacitores se miden por su capacitancia y su unidad es el faradio. Esta unidad tiene sus submúltiplos como:
1 microfaradio = 1 uF = 10^-6 F
1 uF = 1000 nF
1 nanofaradio = 1 nF = 10^-9 F
1 nF = 1000 pF
1 picofaradio = 1 pF = 10^-12 F
Los condensadores de capacitancia pequeña no tienen polaridad y los capacitancia grande son polarizados y se denominan electrolíticos. Se representan simbólicamente de la siguiente manera:

A continuación se presenta los condensadores comerciales con su capacitancia y el voltaje máximo de operación:
La oposición que presenta un condensador a la corriente alterna se denomina Reactancia capacitiva se mide en ohmios y depende del valor del condensador y de la frecuencia. Se representa como Xc.
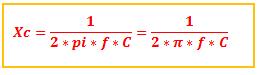
Nótese que si se tiene corriente continua la f = 0, entonces, Xc = infinito (número muy grande) que en términos prácticos quiere decir que un condensador en CC es un circuito abierto.
El voltaje que almacena el condensador o capacitor es igual a su reactancia multiplicada por la corriente.
Vc = Xc * I
CIRCUITO RESISTIVO-CAPACITIVO (Ver video)
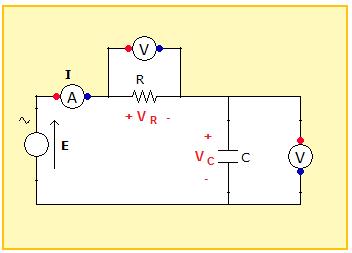
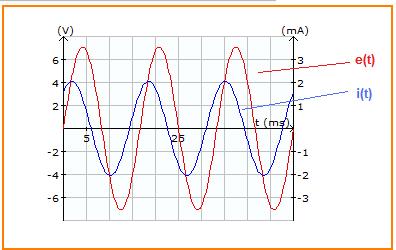
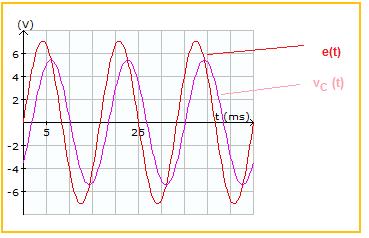
En la figura se tiene una fuente de voltajes de CA conectada a una resistencia R y a un condensador C en serie. Si Erms = 5.0V, f =60 Hz, R=2.2K, C=1.0 uF, las señales de voltaje de la fuente E y de la corriente I se muestran a continuación con un desfasaje entre ellas. Obsérve que la corriente i(t) tiene un desfase positivo (adelantada) con respecto al voltaje de la fuente e(t) que tiene fase de 0 grados.
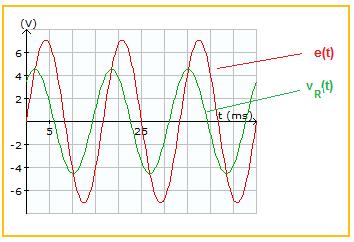
Observe las señales de la fuente y del voltaje en la resistencia. Al igual que la corriente, la señal de voltaje en la resistencia tiene fase positiva (comienza primero) con respecto a la de la fuente.
La señal de voltaje en el condensador está atrasada (comienza después) con respecto a la de la fuente, esto es, que tiene fase negativa, como se aprecia en la figura:
El análisis comúnmente utilizado para analizar circuitos de corriente alterna es el vectorial o fasorial. La combinación de resistencias y elementos capacitvos presenta al paso de la corriente una oposición que se denomina impedancia que se nota como Z y las ecuaciones de cálculo son las siguientes:

Diagrama fasorial:
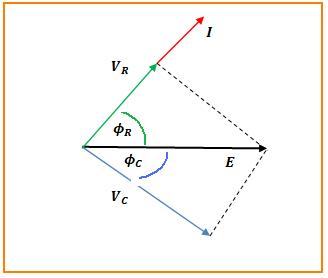
Para los valores dados y teniendo en cuenta que los voltajes en la resistencia y en el condensador está desafasados 90 grados, se tiene:
Erms = 5.0V, f =60 Hz, R=2.2K, C=1.0 uF
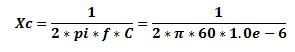
En al calculadora del computador:
2 * pi * 60 * 1.0 Exp 6 +/- = 1/x = respuesta Xc = 2652 ohm = 2.6 Kohm
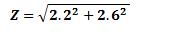
En al calculadora:
2.2 x^2 + 2.6 x^2 = x^y 0.5 = respuesta Z = 3.4 Kohm
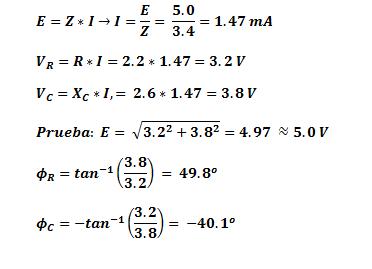
Para el último cálculo se coloca la calculadora en sexagecimal y se hace:
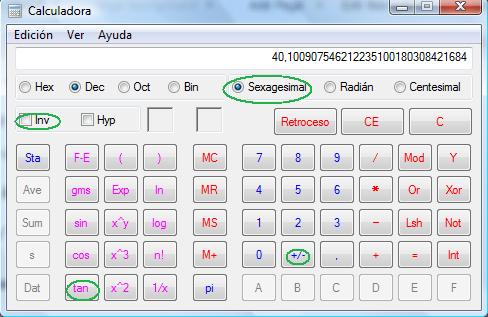
3.2 / 3.8 = inv tan = +/- respuesta - 40.1
