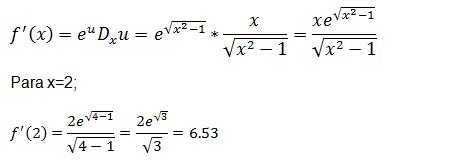DERIVADAS
La derivada de una función y=f(x) con respecto a x, es igual a la variación infinitesimal de la función con respecto a x.
Si y=f(x), entonces,

DERIVADA DE UNA CONSTANTE
La derivada de una constante es cero. f(x)=c, entonces f’(x)=0
Ejemplo:
Hallar la derivada de y=f(x)=5
Si f(x) es una constante entonces, f(x+∆x)=f(x) = 5, por tanto
f(x+∆x)-f(x)=0
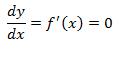
DERIVADA DE UNA POTENCIA
Ejemplo:
Hallar la derivada de y=f(x)=x5
f’(x)=5x5-1 = 5x4
Ejemplo:
Hallar la derivada de f(x)=3x4
f’(x)=3(4x4-1)=3(4x3)=12x3
Ejemplo:
Hallar la derivada de y =f(x)=2x-2
f’(x)=2(-2x -2-1)=2(-2x-3)= -4x-3= -4/x3

Ejemplo:
Hallar la derivada de y=f(x)=3x4+5x3-2x2-6x+2
f(‘(x)=3(4x3)+5(3x2)-2(2x)-6+0 = 12x3+15x2-4x-6
DERIVADA DE UN PRODUCTO
La derivada de un producto de funciones f(x)*g(x)es igual a la derivada del primero f”(x) por el segundo g(x) más el primero f(x) por la derivada del segundo g’(x)

Ejemplo:
y=(2x2-3x)(x3-2x2+3)
f(x)=2x2-3x , entonces, f’(x)=4x-3
g(x)=x3-2x2+3, entonces, g’(x)=3x2-4x+0=3x2-4x
y’= (4x-3)( x3-2x2+3)+( 2x2-3x)( 3x2-4x)
simplificando:
y’=10x4-28x3+18x2+12x-9
La derivada de un cociente f(x)/g(x) es igual a:
Aplicando Scilab: //variable simbólica x x=poly(0,'x') // ejemplo y=x^5; derivat(y) //y'=5x^4 // ejemplo y=3*x^4 derivat(y) //y'=12x^3 // ejemplo y=2*x^-2; D=derivat(y) simp(D) //D=-4/x^3 // ejemplo y=3/x^3; D=derivat(y) simp(D) //D=-9/x^4 // ejemplo y=3*x^4+5*x^3-2*x^2-6*x+2; D=derivat(y) simp(D) //y'=-6-4x+15x^2+12x^3 // ejemplo y=(2*x^2-3*x)*(x^3-2*x^2+3); D=derivat(y) simp(D) //y'=-9+12x+18x^2-28x^3+10x^4 // ejemplo y=(2*x^3+2*x)/(3*x^2-2); D=derivat(y) simp(D) //y’=(-4-18x^2+6x^4) / (4-12x^2+9x^4)
Derivación en cadena. Si y=f(u), u=g(x), entonces, la derivada de y con respecto a x es igual a:
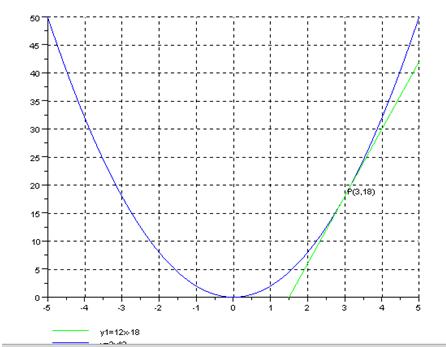
Aplicando Scilab, x=poly(0,'x') y=(x^3-2*x^2-4)^4; D=derivat(y) simp(D) PENDIENTE DE UNA FUNCIÓN La pendiente de una función en un punto es la derivada en ese punto. Ejemplo: Hallar la pendiente de la función y=2x2 en el punto x=3. Hacer las gráficas. Para x=3, entonces, y=2(3)2 = 18 el punto es P(3,18) La pendiente es m=y’=4x = 4(3)=12 Gráficamente la pendiente es la tangente de la recta que pasa por ese punto, su función se obtiene de: y-y1=m(x-x1), donde x1=3, y1=18 y-18=12(x-3), entonces, y=12x-36+18, y=12x-18 Por Scilab, // cálculo de la pendiente en x=3 function y=f(x) y=2*x^2; endfunction x=3; derivative(f,x) //Respuesta: m=12 // gráfica de la parábola y=2x2 y de la recta y1=12x-18 x=[-5:0.1:5]; y=2*x^2; y1=12*x-18; plot2d(x,[y' y1'],[2,3],leg="y1=12x-18@y=2x^2",rect=[-5 0 5 50]) xgrid xstring(3,18,["P(3,18)"])
Una función es implícita cuando para encontrar su y=f(x) se tiene que despejar de la ecuación, por ejemplo: 2x2 - 3y = 4 es una función implícita. Su valor es igual a 2x2-4 = 3y, o sea, y=f(x)=(1/3)(2x2-4) Ejemplo: Para la siguiente ecuación: y3 – 2y2 + 4x = x2 – 2, hallar la derivada y’= f’(x) Derivando la expresión, se tiene, 3y2 y’ – 4y y’ + 4 = 2x – 0, factorizando y’ y’ (3y2 – 4y) = 2x – 4, despejando
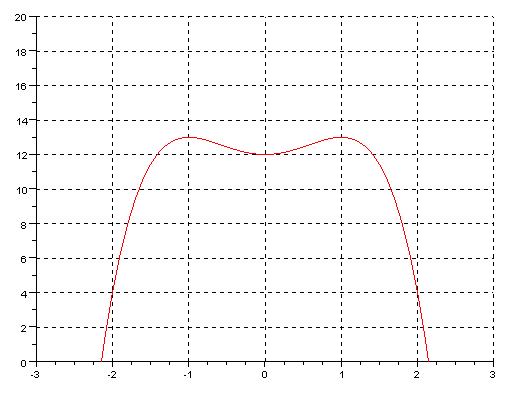
Para encontrar los puntos críticos de una función f(x) se realiza su correspondiente derivación f’(x) y se iguala a cero. Los valores de x que cumplen con esta solución son los puntos críticos. Ejemplo: Sea f(x) = - x4 +2x2 +12, su derivada es, f’(x) = - 4x3 + 4x, igualando a cero, - 4x3 + 4x = 0, factorizando, -4x(x2 – 1) = 0, los valores para los cuales se cumple, son x = 0, x = 1, x = -1 Estos son los puntos críticos, que tienen su derivada igual a cero, o sea, su pendiente = 0 (recta horizontal en el punto) MÁXIMO, MÍNIMO E INFLEXIÓN Un punto crítico puede ser un valor máximo de la función, un valor mínimo o ni lo uno ni lo otro que se conoce como punto de inflexión. Resolver este problema implica calcular la segunda derivada de la función, esto es, la derivada de la primera derivada y considerar lo siguiente: Si f’’(x) > 0 estamos en un punto mínimo Si f’’(x) < 0 estamos en un punto máximo y Si f’’(x) = 0 es un punto de inflexión Ejemplo: Continuando con el ejemplo anterior, Primera derivada: f’(x) = -4x3 +4x Segunda derivada f’’(x) = -12x2 +4 Reemplazando los valores de los puntos críticos, Para x = 0, f’’(0)= -12(0)2 +4 = 4 > 0 es un punto mínimo Para x = 1, f’’(1)= -12(1)2 +4 = -8 < 0 es un máximo Para x = -1, f’’(-1)= -12(-1)2 +4 = -8 es un mínimo Programa en Scilab: // cálculo de máximo y mínimos // variable simbólica x x=poly(0,'x') fx=-x^4+2*x^2+12; // primera derivada df=derivat(fx) // df=-4x^3+4x // cálculo de puntos críticos p=[-4 0 4 0]; r=roots(p) //puntos críticos=0 -1 1 //cálculo de la segunda derivada d2f=derivat(dy) //d2f=-12x^2+4 //cálculos de d2y en los puntos críticos x=0; d2f0=-12*x^2+4 x=1; d2f1=-12*x^2+4 x=-1; d2fm1=-12*x^2+4 //d2f(0)=4, d2f(1)=-8, d2f(-1)=-8 //gráfica de la función x=[-3:0.1:3]; fx=-x^4+2*x^2+12; plot2d(x,fx',5,rect=[-3 0 3 20]) xgrid
La derivada con respecto a x de una función logaritmo natural denotada como f(x)= ln(x), está dada por:
PROPIEDADES DE LOS LOGARITMOS a) Ln(a * b) = ln(a) + ln(b) b) Ln(a / b) = ln(a) - ln(b) c) Ln(a n) = n * ln(a) Ejemplo: Hallar la derivada de:
La función exponencial es la inversa del logaritmo natural. Se nota como exp
Aplicando Scilab: //definición de la función function y=f(x) y=exp(sqrt(x^2-1)); endfunction //cálculo de la derivada en x=2 df=derivative(f,2) // df = 6.527 FUNCIONES TRIGONOMÉTRICAS Las fórmulas para el cálculo de las derivadas de las funciones trigonométricas son: sen(x) cos(x) sen u cos u Dx u cos(x) -sen(x) cos u -sen u Dx u tan(x) sec2(x) tan u sec2 u Dx u cot(x) -csc2(x) cot u -csc2 u Dx u sec(x) sec(x)tan(x) sec u sec u tan u Dx u csc(x) -csc(x)cot(x) csc u -csc u cot u Dx u
Por Scilab: //definición de la función function y=f(x) y=cos(x)/(1+sin(x)); endfunction //pasar ángulo a radianes x=30*%pi/180; //calcular la derivada dy=derivative(f,x) // dy = 0.667
DERIVADA DE UN COCIENTE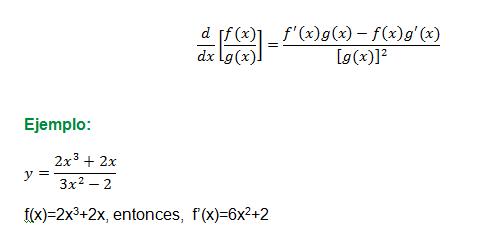

DERIVACIÓN EN CADENA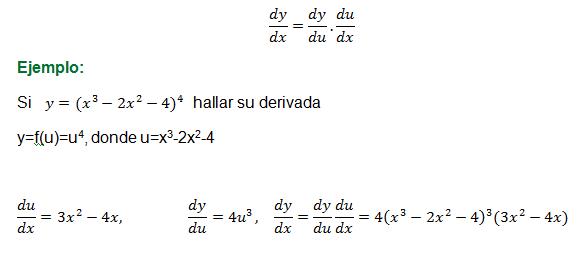
DERIVACIÓN IMPLÍCITA
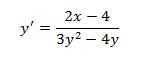
PUNTOS CRÍTICOS DE UNA FUNCIÓN
FUNCIONES LOGARÍTMICAS Y EXPONENCIALES

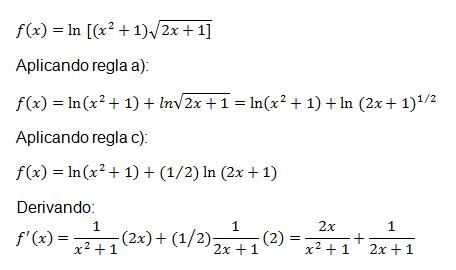

FUNCIÓN EXPONENCIAL