2. FUNCIONES EN SCILAB
Función Exponencial: Se ejecuta con el comando exp
Ejemplo
Para x = 2.78, calcular

En Scilab se resuelve,
--> x = 2.78;
--> y = 2.3*exp (1.8*x)
y =
342.7184
Logaritmo natural: Se ejecuta con el comando log
Ejemplo:
Hallar el valor de la expresión: 3.6 ln(35.8),
Con Scilab se resuelve,
--> x = 35.8;
--> y = 3.6*log(x)
y =
12.880612
Logaritmo decimal: Se ejecuta con el comando log10
Ejemplo:
Hallar el log(123.89),
En Scilab,
--> x = 123.89;
-->y = log10(x)
y =
2.0930363
FUNCIONES TRIGONOMÉTRICAS
Scilab puede calcular las funciones trigonométricas seno, coseno, tangente, cotangente. El ángulo debe darse en radianes, por lo tanto si el ángulo se da en grados debe convertirse en radianes usando la fórmula:

El valor de pi es aproximadamente 3.1416 y en Scilab simplemente se escribe %pi
-->a=%pi
a =
3.1415927
TABLA DE LAS FUNCIONES
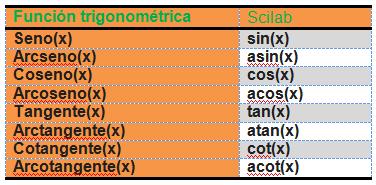
Nota: Los comandos de Scilab siempre se escriben en minúsculas
Ejemplo:
Para un ángulo de 450 hallar sus funciones trigonométricas
Programa en Scilab:
-->// pasar grados a radianes
-->g=45;
-->r=g*%pi/180
r =
0.7853982
-->// calcular seno
-->sin(r)
ans =
0.7071068
-->// calcular coseno
-->cos(r)
ans =
0.7071068
-->// calcular tangente
-->tan(r)
ans =
1.
Ejemplo:
Para el triángulo rectángulo de la figura su hipotenusa es igual a c = 8.3 y el cateto b = 4.5. Encontrar el valor del otro cateto y el ángulo que forman.

Programando en Scilab,
--> // valores conocidos
--> c=8.3;
--> b=4.5;
--> // cálculo del cateto a
-->a=sqrt(c^2-b^2)
a =
6.9742383
--> // cálculo del ángulo
-->beta=asin(b/c)
beta =
0.5730159
--> // pasar valor a grados
-->ang=beta*180/%pi
ang =
32.831392
La respuesta al problema es que el otro cateto vale 6.97 y el ángulo es de 32.8o
EVALUACIÓN DE UNA FUNCIÓN
Cualquier función f puede ser evaluada, reemplazando sus valores en la ecuación.
Ejemplo:
Para x=2.5, y=3.2 evaluar la función

Se evalúa con Scilab así,
--> // valores de las variables
-->x=2.5;
-->y=3.2;
--> // cálculo de la función
-->f=sin(2*x)-2*cos(y)+sqrt(3^x)
f =
4.9858873
SOLUCIÓN DE ECUACIONES
Para solucionar una ecuación se utiliza el comando roots aplicado a un polinomio construido con los coeficientes de la ecuación.
Ejemplo:
Hallar las raíces de la ecuación x2 + 3x +2 = 0
Programa Scilab
-->// polinomio creado con los coeficientes de la ecuación
-->p=[1 3 2];
-->// raíces de la ecuación
-->raices=roots(p)
raices =
- 1.
- 2.
La ecuación es de orden 2 (exponente más alto), por tanto tiene dos raíces o soluciones que son: x1 = - 1, x2 = - 2
Ejemplo:
Encontrar las raíces de la ecuación 2x3 – 4x + 3 = 0
Programa Scilab,
-->// polinomio creado con los coeficientes de la ecuación
-->p=[2 0 -4 3];
-->// raíces de la ecuación
-->r=roots(p)
r =
0.8490240 + 0.4031444i
0.8490240 - 0.4031444i
- 1.6980481
Como es una ecuación de orden 3 tiene entonces tres raíces o soluciones a la ecuación, en este caso tiene dos números complejos y un real.
x1=0.84=0.40i, x2=0.84-0.40i, x3=- 1.69
Consultas o preguntas sobre esta unidad pueden hacerlas a ceduvirt@gmail.com
Terminada esta unidad puede pasar a ver el módulo de los laboratorios correspondientes. Clic aquí