INTEGRALES
Es una de las herramientas más importantes del cálculo que permite calcular áreas bajo una curva, áreas que generan una curva en revolución y volúmenes de sólidos.
INTEGRAL DEFINIDA
Se define como el área bajo la curva de una función f(x) en un intervalo entre dos límites [a, b]. Se nota de la forma:
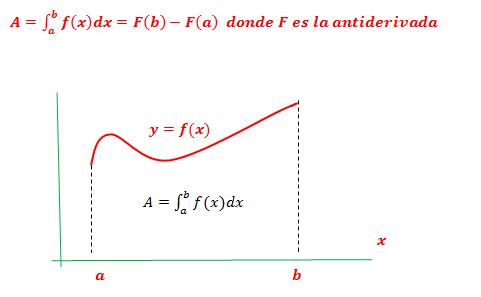
INTEGRAL DE UNA CONSTANTE
La integral de una función es la antiderivada de la función (Teorema fundamental del Cálculo). Esto quiere decir, que si y = cx, entonces, y’= c, o sea que, la antiderivada de una constante c es cx.

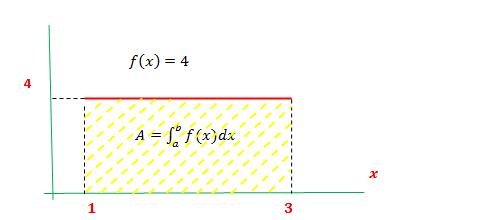
Como se observa el área mostrada es un rectángulo de ancho igual a 2 = 3-1 y de alto igual a 4. Su A = 2x4 = 8
Prueba con Scilab:
//definición de la función
function y=f(x)
y=4
endfunction
//calcular la integral entre x=1 y x=3
intg(1,3,f)
// ans = 8
INTEGRAL DE UNA POTENCIA
Con Scilab:
//definción de la función
function y=f(x)
y=x^4
endfunction
// calculo de la integral
intg(2,5,f)
//ans = 618.6
Ejemplo:
Hallar la integral de la función y = 2x3 - 3x2 + 5x - 3 entre x=1 y x=4
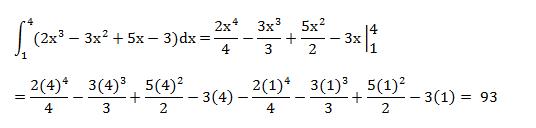
Programa Scilab:
//definción de la función
function y=f(x)
y=2*x^3-3*x^2+5*x-3
endfunction
// cálculo de la integral
intg(1,4,f)
//ans=93
INTEGRAL INDEFINIDA
La integral indefinida se define como:

FUNCIONES LOGARÍTMICAS
La integral de una función de la forma f(u)=1/u es igual a:

Cálculo por Scilab:
//definir función
function y=f(x)
y=2*x/(4*x^2+1);
endfunction
//calcular la integral
I=intg(1,2,f)
// I = 0.3059
FUNCIONES TRIGONOMÉTRICAS
Las integrales de las funciones trigonométricas son sus correspondientes antiderivadas.
Ejemplo:
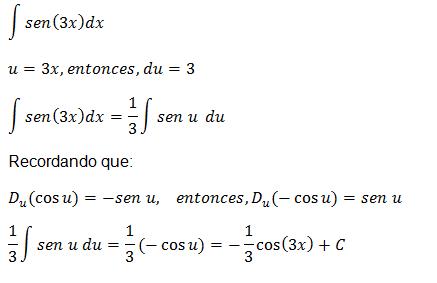

Por Scilab:
//definir función
function y=f(x)
y=csc(sqrt(x))^2/sqrt(x);
endfunction
//calcular integral
i=intg(0.5,1.5,f)
// i = 1.619
