FÍSICA MECÁNICA
1. CINEMÁTICA
Física es una ciencia dedicada al estudio de los fenómenos naturales. Su comprensión requiere el uso de las matemáticas que sustenta los conceptos físicos como el de fuerza, energía, la hidráulica, la termodinámica, el electromagnetismo, etc. La cinemática estudia el movimiento de los cuerpos sin importar la causa que lo produce.
Las cantidades físicas fundamentales son la longitud, masa, tiempo, temperatura y carga. Todas las demás cantidades físicas se pueden expresar en función de estas cantidades físicas fundamentales y sus mediciones dependen según el Sistema Internacional de Medidas del metro (m), kilogramo (kg), segundo (sg), grado kelvin (ºk) y del coulomb (coul).
MOVIMIENTO RECTILÍNEO
Movimiento rectilíneo de una partícula es aquel cuya trayectoria es una línea recta y su posición cambia al transcurrir el tiempo.
DESPLAZAMIENTO
Al cambio de posición se le denomina desplazamiento y se nota como:
∆x = x – xo
donde x es la posición final y x0 es la posición inicial (origen O).
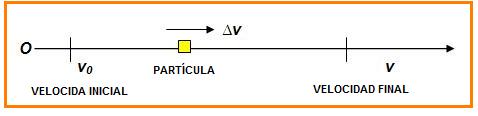
VELOCIDAD
La velocidad media definida entre dos posiciones en los instantes t y t0 es igual al cambio de desplazamiento con respecto al cambio del tiempo y está definida por :
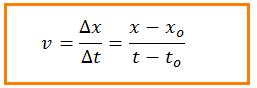
La velocidad instantánea es la velocidad de la partícula en un instante dado. Para ello se hace el intervalo de tiempo muy pequeño ∆t y calcular la velocidad en el límite cuando ∆t --> 0, esto es:
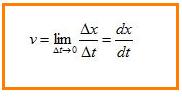
La velocidad es la derivada del desplazamiento.
ACELERACIÓN
La aceleración media definida entre dos instantes t y t0 es igual al cambio de velocidad con respecto al cambio del tiempo y está definida por :
La aceleración instantánea es la aceleración de la partícula en un instante dado. Para ello se hace el intervalo de tiempo muy pequeño ∆t y calcular la aceleración en el límite cuando ∆t --> 0, esto es:
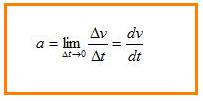
La aceleración es la derivada de la velocidad.
EJEMPLO 1:
La posición de una partícula en metros con respecto al tiempo varía según la siguiente ecuación :
x = t3 + 5t2 + 3t + 4
calcular (a) su velocidad y (b) su aceleración en t =1 sg y en t = 4 sg
Solución:
a) Derivando la ecuación de la posición:
Para t = 1 sg, reemplazando t por el valor de 1, se tiene que : v = 3(1)2 + 10(1) + 3 = 16 m/sg
Para t = 4 sg, reemplazando t por el valor de 4, se tiene que : v = 3(4)2 + 10(4) + 3 = 91 m/sg
b) Derivando la ecuación de la velocidad:
Para t = 1 sg, se tiene que : a =6(1) +10 = 16 m/sg2
Para t = 4 sg, se tiene que : a =6(4) +10 =34 m/sg2
Programa en Scilab:
clear//cálculo de la velocidadt=poly(0,'t')x = t^3 +5*t^2 +3*t+4;v=derivat(x)//nos da como respuesta//v=3+10*t+3*t^2//****************************************clear// cálculo de la velocidad en t=1 y t= 4 sgfunction x=f1(t)// ecuación de la posiciónx = t^3 +5*t^2 +3*t+4;endfunctiont = 1;v1 = derivative(f1,t)t = 4;v2 = derivative(f1,t)// nos da v1=16 y v2=91//****************************************// cálculo de la aceleracióncleart=poly(0,'t')v=3+10*t+3*t^2;a=derivat(v)//nos responde que a=10+6*t//****************************************clear// cálculo de la aceleración en t=1 y t= 4 sgfunction v=f2(t)// ecuación de la posiciónv=3+10*t+3*t^2;endfunctiont = 1;a1 = derivative(f2,t)t = 4;a2 = derivative(f2,t)// nos da a1=16 y a2=34
MOVIMIENTO RECTILÍNEO UNIFORME
Un movimiento rectilíneo uniforme es aquel que tiene una trayectoria recta y la velocidad constante, o sea , una aceleración igual a cero.
Si t0 =0, entonces, x = x0 + v t
EJEMPLO 2:
Un automóvil va a una velocidad constante de 200 Km / hr . Si se acciona un cronómetro cuando pasa por una posición de 50 Km a qué posición llegará después de 3 horas de recorrido?
Solución :
xo = posición inicial = 50 km
v = velocidad = 200 km/hr
t = tiempo = 3 hr
reemplazando:
x = x0 + v t =50 Km + 200 Km/hr (3 hr) = 50 km + 600km = 650 km
Respuesta: Ha llegado a la posición 650 Km pero en 3 horas sólo ha recorrido: 650 - 50 = 600 km
Caso especial: Si la posición inicial es x0 = 0 entonces simplemente,
x = v t
MOVIMIENTO UNIFORME ACELERADO
Un movimiento uniformemente acelerado es aquel que tiene su aceleración constante. Partiendo de la ecuación vista anteriormente,
Por tanto, si t0 = 0, entonces:
Si la posición inicial es cero:
De las dos ecuaciones anteriores, podemos sacar una tercera que relacione velocidad, aceleración y espacio:
v = vo + at , despejando t = (v – v0) /a, reemplazando,
x = v0 [v – v0) /a] + ½ a[v – v0) /a] 2
x = [v0 v – v0 2 ] /a + ½ [v2 –2v v0 +v0 2 ] /a
2ax = v2 – v0 2 ⇒ v2 = v0 2 +2ax
EJEMPLO 3:
Un móvil pasa por un punto a una velocidad de 80 k/hr. Si va con una aceleración constante de 20 km/hr ¿Cuánto recorrerá al cabo de 4 hr?
Solución:
vo = 80 km/hr;
a = 20 km/hr2
t = 4 hr
reemplazando:
x = vo* t + (1/2)*a*t^2 = 80*4 + (1/2)(20)*(4^2) = 320 + 10*16 = 320 +160 = 480 km
EJEMPLO 4:
Un motociclista parte del reposo y recorre una distancia de 300 km a una aceleración constante de 100 km/hr2 . ¿Cuál fue su velocidad de llegada?
Solución:
Como parte del reposo, entonces v0 = 0, además, x = 300 km, a = 100 km/hr2
x = v0 t +½ a t2
300 = 0 + (1/2)* (100 )(t^2 ), entonces, 300 = 50 (t2)
despejando se tiene, t2 = 300 / 50 = 6 , luego t = sqrt(6) = 2.45 hr
ya conocido el tiempo, v = 0 + a t = (100 )(2.45 ) = 245 km / hr
Otra forma: v2 = v0 2 +2ax ⇒ v2 =0 2 +2(100 )(300)
v2 =60.000 ⇒ v = sqrt(60.000) = 245 km/hr
Respuesta: La velocidad de llegada es de 245 km/hr
MOVIMIENTO DE CAÍDA LIBRE
Si no se tiene en cuenta la fricción del aire todos los cuerpos caen dirigidos hacia el centro de la tierra con movimiento uniformemente acelerado con una aceleración cuyo valor es igual a la gravedad, esto es, g = 9.8 m/sg2. Lo contrario, hacia arriba los cuerpos se desaceleran hasta llegar a al posición de reposo con una aceleración igual a g = - 9.8 m /sg2. Si consideramos hacia arriba el movimiento denotado con la variable y , se tiene que las ecuaciones son las siguientes:
Movimiento desacelerado Movimiento aceleradoy = v0 t -½ g t2 y = v0 t +½ g t2
v = v0 – g t v = v0 + g t
En el movimiento desacelerado la dirección del movimiento (arriba) y la gravedad (abajo) están en sentido contrario, en el acelerado el movimiento (abajo) y la gravedad (abajo) tienen el mismo sentido.
EJEMPLO 5 :
Se deja caer un objeto desde un edificio de 500 m de altura. Calcular (a) la velocidad y (b) el tiempo que tarda en llegar al suelo.
Solución:
Variables conocidas: y = 500 m, v0 = 0, g = 9.8 m/sg2
(a) El movimiento es de caída libre, entonces es un movimiento acelerado:
y = v0 t +½ g t2 = 0 +½ (9.8 ) t2 = 4.9*t^2 = 500
despejando : t2 = (500 )/(4.9) = 102.04 , t = sqrt(102.04) = 10.1 sg
Respuesta: El tiempo que tarda en llegar al suelo es de 10.1 sg
(b) Conocido el tiempo se puede hallar la velocidad final:
v = v0 + g t, v = 0 + (9.8)(10.1) = 98.99 m/sg
Respuesta: La velocidad con que llega al suelo es de aproximadamente 99 m/sg
EJEMPLO 6:
Se lanza un objeto hacia arriba con una velocidad de 50 m/sg . Calcular la máxima altura que alcanza y el tiempo que gasta.
Solución:
Variables conocidas: v0 = 50 m/sg, v = 0 (velocidad final)
El movimiento es desacelerado (hacia arriba), entonces:
v = vo - g t, 0 = 50 - (9.8)t , por tanto, t = 50/9.8 = 5.1 sg
y = vo t -½ gt2 = (50)*(5.1) - (1/2)* (9.8)*(5.1^2) = 255 – 127.45=127.55 m
Respuesta : La altura que alcanza es de 127.55 m y gasta un tiempo de 5.1 sg
MOVIMIENTO EN PLANO INCLINADO
El movimiento de un cuerpo en un plano inclinado es un movimiento uniforme acelerado cuya aceleración depende de la aceleración de la gravedad y del ángulo de inclinación del plano. Si se tiene un plano inclinado de 30º como el de la figura:
La aceleración del bloque es:
Se observa que se forma un triángulo rectángulo entre la aceleración del bloque (plano inclinado, la gravedad (vertical) y el suelo (horizontal). recordando que el seno de un ángulo lo forma el cociente entre el lado opuesto y la hipotenusa, o sea:
sen(30) = opuesto/hipotenusa = g/a, despejando la aceleración,
a = g sen 30º
En general:
a = g sen α
donde α es el ángulo de inclinación del plano.
Las ecuaciones que rigen el movimiento de un cuerpo en un plano inclinado son entonces:
(a) Hacia arriba. (b) Hacia abajo
e = v0 t -½ (g sen α) t2 e = v0 t +½( g sen α) t2
v = v0 – (g sen α) t v = v0 +( g sen α) t
EJEMPLO 7:
Sobre un nevado de pendiente de 60º ( plano inclinado de 60º) un alpinista se suelta del reposo. Calcular la velocidad de llegada y el tiempo que tarda en recorrer 500 m.
Solución:
e = vo t +½( g sen α) t2 , 500 = 0 + (1/2)*9.8* (sen 60) t2
500 = 4.9(0.866)t2 , 500 = 4.24t2
t2 = 500 / 4.24=111.92 sg , t = sqrt(111.92) = 10.85 m/sg
v = vo* +( g sen α) t = 0 +(9.8*sen60) t = 0 + 9.8(0.866)(10.85) = 92.1 m/sg
MOVIMIENTO CIRCULAR
Movimiento circular uniforme es aquel cuya trayectoria es una circunferencia y la magnitud de la aceleración es constante.
θ = desplazamiento angular, ω = velocidad angular, α = aceleración angular
Las ecuaciones que relacionan posición, velocidad y aceleración angular son :
Si α = constante y t0 = 0, θ0 = 0, entonces:
ω = ωo + α t , θ = ω o t + ½ α t2
Si α = 0, o sea que la velocidad angular es constante, entonces : α = 0
θ = ω t
EJEMPLO 8:
Una rueda gira a 8 rpm (revoluciones por minuto). Si la velocidad angular es constante, calcular su posición angular después de 5 segundos.
Solución:
1 minuto = 60 seg y una revolución tiene 360 grados
ω = 8 rpm = 8 rev / min = (8 rev/min) (1 min/60 sg),
= 0.13 rev /sg = 0.13 (360º/rev) = 46.8º/sg
θ = ω t = (46.8º/sg)(5 sg) = 234º = 234º
como 180º es igual a π radianes (= 3.14),
ω = (46.8º/sg)(3.14/180) = 0.82 rad/sg
θ = 234º(3.14/180º) = 4.1 rad
Respuesta: ω = 0.82 rad/sg , θ = 4.1 rad
EJEMPLO 9:
La aceleración de una partícula con movimiento uniformemente acelerado es de 25 rad/sg2, calcular su posición si parte del reposo en θ =0 y su velocidad después de 1 minuto.
Solución:
Variables conocidas : ω0 = 0, α = 25 rad/sg2, t = 60 sg
ω = ω0 + α t = 0 +(25 rad/sg2)(60 sg) = 1500 rad/sg
θ = ω 0 t + ½ α t2 = 0 +½(25 rad/sg2)(60sg)2 = 12.5(3600) = 45000 rad
Respuesta: θ = 45000 rad, ω = 1500 rad/sg
ACELERACIÓN TANGENCIAL Y NORMAL
En un movimiento circular la aceleración tiene dos componentes: una debido al cambio de dirección de la velocidad llamada aceleración normal y su vector está dirigido al centro de la circunferencia y otra al cambio de magnitud de la velocidad llamada aceleración tangencial y su vector es tangente a la trayectoria circular. v = w*r
aT : aceleración tangencial, aN : aceleración normal
EJEMPLO 10:
Una cuerpo gira circularmente con radio = 20 cm a una aceleración angular de 50 rad/sg2. Para t = 10 sg calcular su aceleración tangencial y normal si partió del reposo.
Solución:
Respuesta : La aceleración tangencial es de 1.05 m/sg2 y la aceleración normal es de 5.47 m/sg2












